What is the resistance
2021-10-03 05:12:21
1 Answer
You did not provide required values to solve this question. but we will assume some of them to make it easy for you solving such types of questions.
The area of the bar along the length can be find as
Now putting all the values in eq. 1, we get
To find the resistance of a conductor either circular or rectangular by given resistivity, length and area. we can use the following equation to find resistance:
$$R = \rho {l \over A} \tag{1}$$
$$\text{where} \, \rho = resistivity \\l=length \\A = Area$$
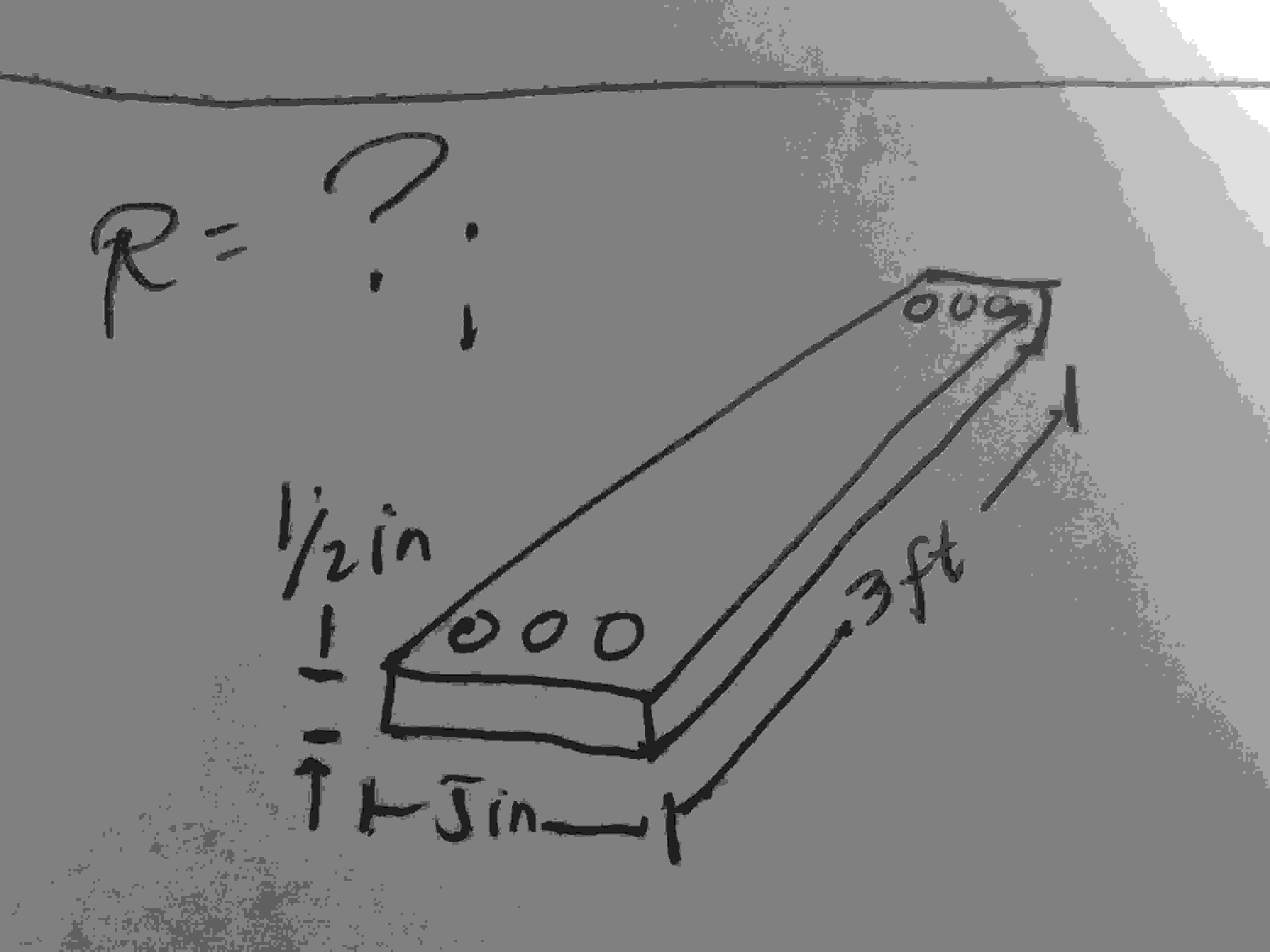
let assume that the bar in the given image is a copper bus-bar, as used in
the power distribution panel of a high-rise office building, with the
dimensions indicated in the image.
$$length = 3 ft\\width = 5in. = 5000 mils\\height= 1/2 in. = 500mils\\\rho = 10.37 CM.ohm /ft \,\text{(copper bar)}$$
To find area in circular mils from a conductor not given in circular shape, we have to use
$$1 \,CM ={\pi \over 4} sq. mils\\1sq.mil = {4\over \pi} \text{CM}$$
$$A_{sq} = width \times height \\= 5000mils \times 500mils\\=2.5\times10^6 sq. mils\\= (2.5\times10^6) (1 \,sq. mils)\\=(2.5\times10^6) ({4 \over \pi} \, CM)\\A_{CM} =3.185\times10^6 \, CM$$
$$\begin{split}R &= (10.37 \,CM.\Omega /ft) {3\,ft \over 3.185\times10^6 \, CM} \\&= 9.768 \times10^{-6} \Omega \\\end{split}$$
2021-10-07 12:17:07
Be the first to comment here!
Do you want to say or ask something?